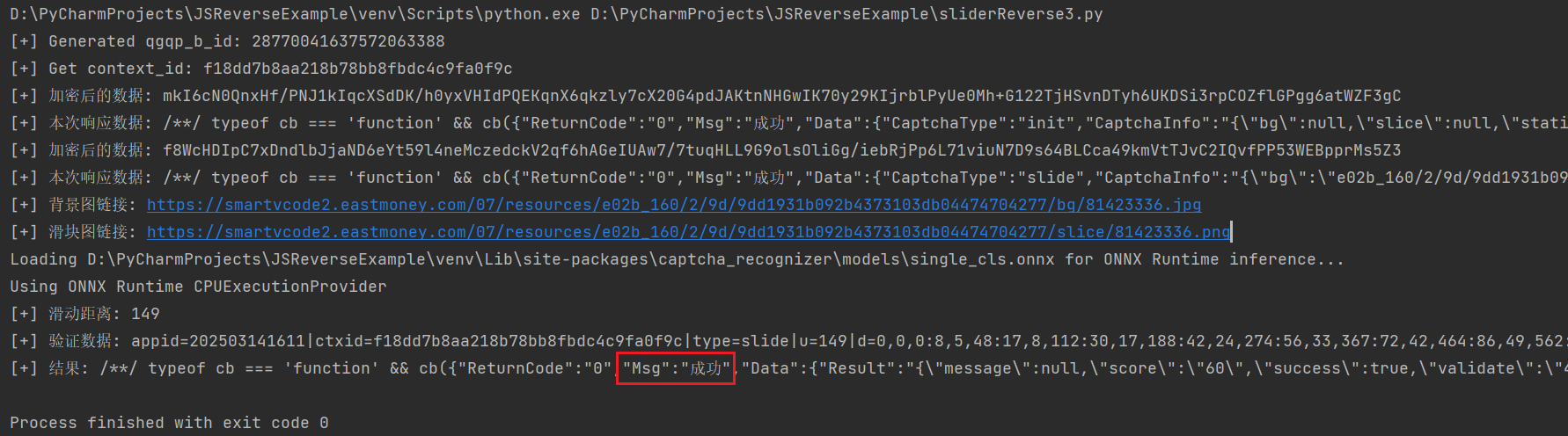
某网站登陆滑块逆向-3

JS逆向

目标：aHR0cHM6Ly9pLmVhc3Rtb25leS5jb20vd2Vic2l0ZWNhcHRjaGEvc2xpZGVydmFsaWQ=

参考文章，直接给了一个滑块的地址，不错的，可以直接分析

初步调试

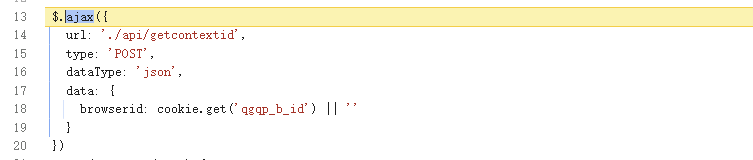
初步调试发现首先会获取contextid这个参数，

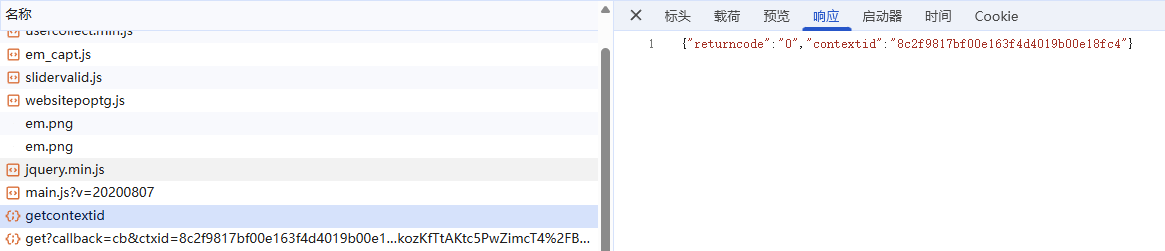
然后get请求就是获取图片地址的请求，

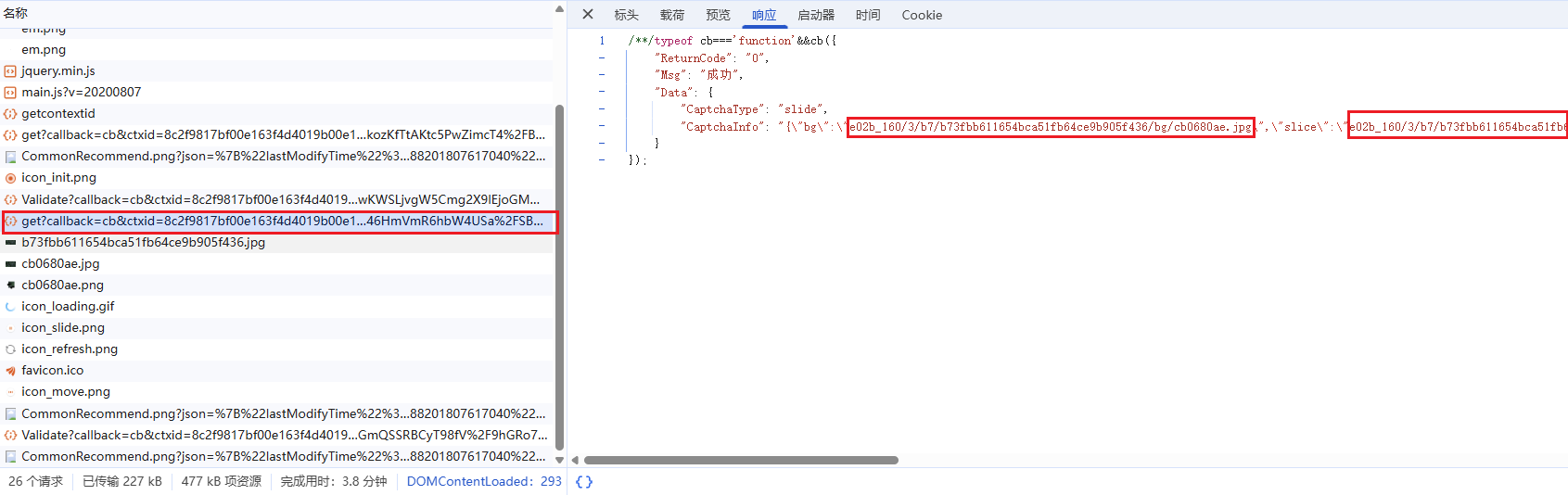
查看get请求的启动器，打上断点，逐步调试

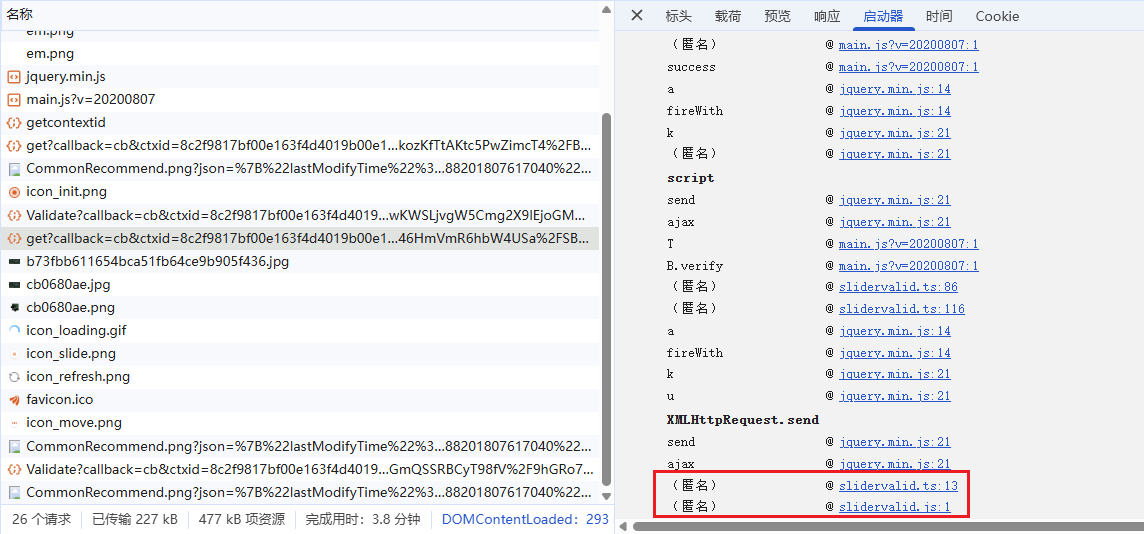
发现这里有获取浏览器cookie的操作，名为qgqp_b_id

可以发现getcontextid请求里带上的browserid就是上面获取的qgqp_b_id

核心部分

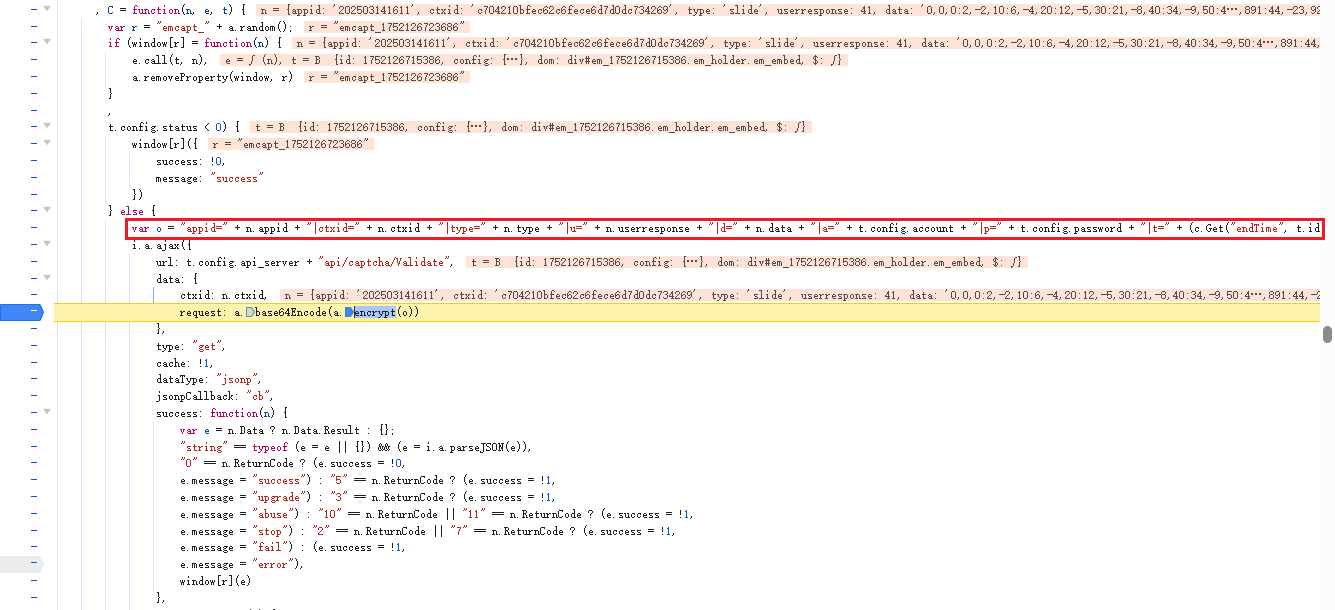
继续调试发现找到了get请求发出的地方：

发出的加密request参数的明文是如下这样组成的，这里变动的其实只有ctxid和r，其他似乎和版本以及测试账号有关

1
2
var u = "appid=" + n.config.appid + "|ctxid=" + n.config.captchaContextId + "|a=" + n.config.account + "|p=" + n.config.password + "|r=" + Math.random();
// eg: appid=202503141611|ctxid=a43299db05b9e1b27570662648f8792d|a=quoteapi|p=|r=0.8229204422883762

再往下走，就是分析加密方法了

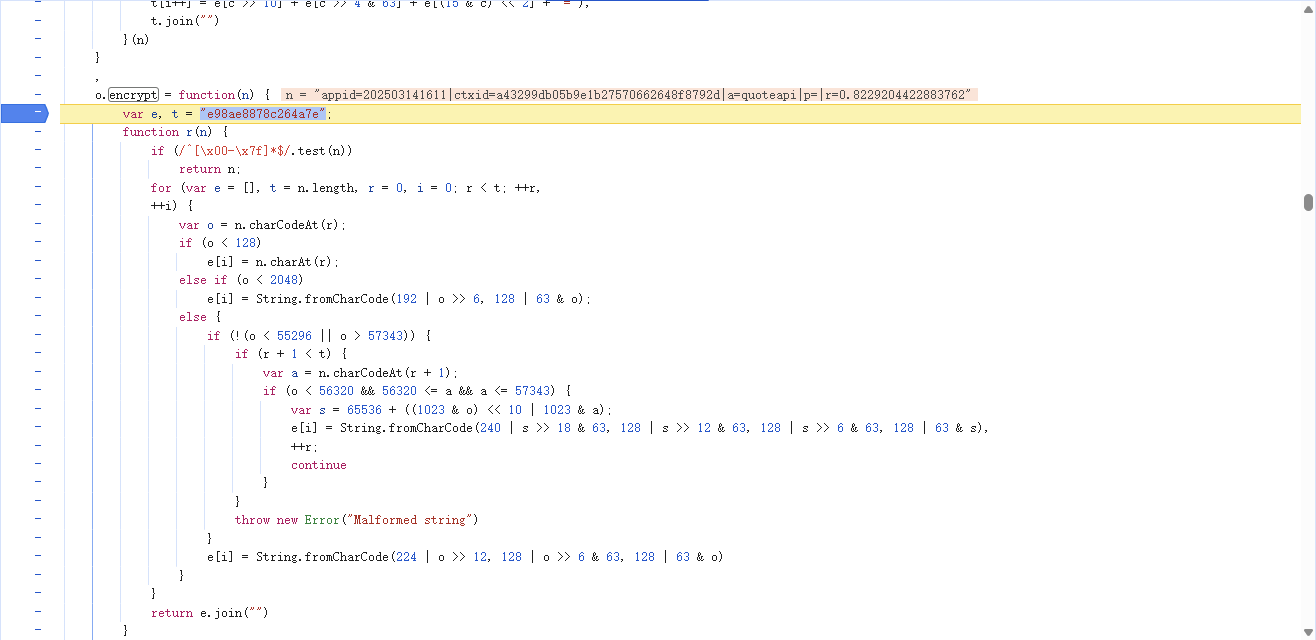
将加密代码发给GPT，推断为XXTEA算法，故验证如下

直接调用JS接口加密结果：

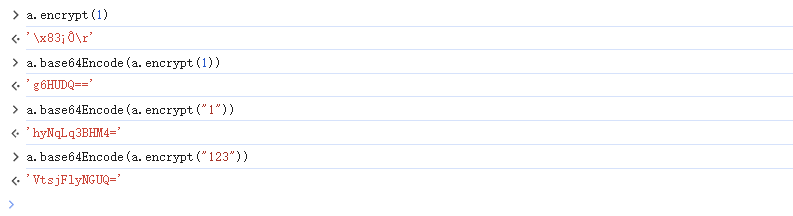
某网站加密结果：

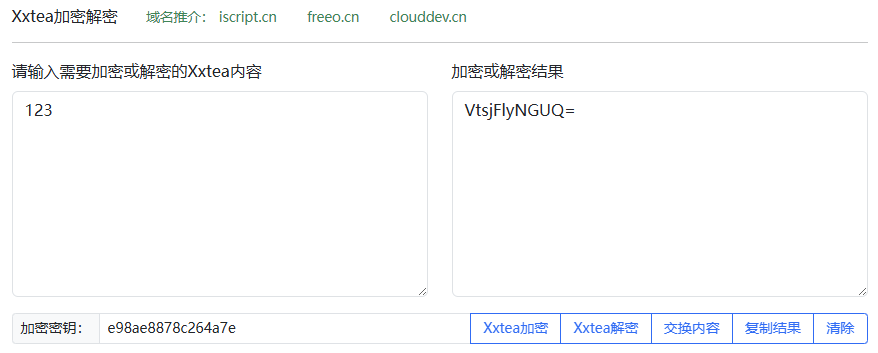
现在可以确认采用了XXTEA算法进行加密

cookie生成

在编写代码时发现cookie不能通过request请求得到，发现是由客户端生成，全局搜索qgqp_b_id，发现其生成逻辑：

  • e 是一个长度为 20 的字符串。第一个字符是一个 1 到 9 的随机数字（由 Math.floor(9 * Math.random() + 1) 生成），接下来的 19 个字符是 0 到 8 的随机数字（由 Math.floor(9 * Math.random()) 生成）。
  • 最终生成的字符串类似 2 + "345678910111213..."，也就是说一个以 1-9 开头，后面跟随 19 个 0-8 的数字的字符串。

设置 cookies：

  • 使用 o.set("qgqp_b_id", e, 1e4, ".eastmoney.com") 将生成的 e 存入名为 qgqp_b_id 的 cookie 中，并设置过期时间为 1e4（即 10,000 秒，约为 2.8 小时），作用域为 .eastmoney.com。
  • 如果当前的 hostname 包含 dingqibao.com.cn 或 dingqibao.cn，还会在相应的域名下设置相同的 cookie。

背景图还原

发现返回的背景图是经过切割后的图片并且没有后续请求进行还原，那么说明是客户端进行还原并显示的。再接收到图片地址请求成功后，我们逐步调试到如下位置，发现DecodeImg方法，

进入k方法，

下面就是背景图还原的方法，经过多次调试发现数组a是一组定值，那么切片位置的还原就依赖于下面的代码：

1
2
3
4
5
6
7
8
for (var l = 0, d = a.length; l < d; l++) {
    var u = "-" + (a[l] % 26 * 12 + 1) + "px " + (a[l] <= 25 ? (0 - i.config.height) / 2 : 0) + "px"
      , p = s.cloneNode();
    p.style.backgroundImage = "url(" + e + ")",
    o.push(p),
    r.appendChild(p),
    p.style.backgroundPosition = u
}

根据实际值用py给出复原代码，注意网站前端将图片缩放为260*160

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def genCompleteImg():
    # 数组a写死
    a = [39, 38, 48, 49, 41, 40, 46, 47, 35, 34, 50, 51, 33, 32, 28, 29, 27, 26, 36, 37, 31, 30, 44, 45, 43, 42, 12, 13,
         23, 22, 14, 15, 21, 20, 8, 9, 25, 24, 6, 7, 3, 2, 0, 1, 11, 10, 4, 5, 19, 18, 16, 17]
    bg_image = requests.get(url=bg_img, headers=headers).content
    # 背景图的高度为160
    height = 160
    image = Image.open(BytesIO(bg_image))
    slices = []
    # 模拟背景图切割过程
    for l in range(len(a)):
        # 计算横向偏移
        x_offset = a[l] % 26 * 12 + 0.4
        # 计算纵向偏移
        if a[l] <= 25:
            y_offset = height // 2
        else:
            y_offset = 0
        left = x_offset
        upper = y_offset
        right = left + 12
        lower = upper + 80
        # 裁剪图像并保存
        cropped_img = image.crop((left, upper, right, lower)).resize((10, 80), Image.Resampling.LANCZOS)
        slices.append(cropped_img)
    columns = 26
    rows = 2
    # 创建一张空白图像，大小为每个小块宽度 * 列数，高度 * 行数
    result_image = Image.new("RGB", (columns * 10, rows * 80))

    # 将切割的小块拼接到新图像中
    for i, slice_ in enumerate(slices):
        row = i // columns
        col = i % columns
        x_position = col * 10
        y_position = row * 80
        # 将切割图像粘贴到拼接图像的指定位置
        result_image.paste(slice_, (x_position, y_position))

    # 保存拼接后的图像
    result_image.save("3_combined_image.jpg")

下面是复原的图片，略有瑕疵

滑动轨迹

打上断点，手动滑动滑块。得到发送的轨迹数据，格式为x1,y1,t1:x2,y2,t2，

1
appid=202503141611|ctxid=d65781be7e6f60636c54a2613b51b4fd|type=slide|u=100|d=0,0,0:0,-2,11:0,-4,37:3,-4,47:7,-6,58:13,-7,69:19,-7,79:25,-7,90:29,-7,101:30,-7,112:31,-7,134:33,-7,150:36,-6,161:41,-6,171:46,-6,181:50,-6,192:53,-6,203:55,-6,237:56,-6,279:57,-6,465:59,-6,476:62,-6,487:66,-6,497:70,-6,507:75,-6,517:80,-6,527:85,-6,537:89,-6,549:92,-6,560:95,-6,570:97,-6,582:99,-6,595:100,-6,610:102,-6,621:101,-6,754:99,-6,764:98,-6,805:98,-7,871:96,-7,881:95,-8,898:96,-8,1038:99,-9,1055:101,-9,1067:103,-9,1084:105,-9,1097:106,-10,1107:105,-10,1298:103,-10,1324:102,-10,1337:101,-10,1353:100,-11,1589:99,-12,1602:97,-12,1616:96,-13,1665:97,-13,1870:100,-14,1882:101,-14,1893:100,-14,2058:98,-14,2069:99,-14,2824:100,-14,2953:100,-14,3191|a=quoteapi|p=|t=3191|r=0.8340204233087531

需要自己补充的字段包括ctxid、u滑动距离、d滑动轨迹数据、t滑动时间、r随机数，

用三阶贝塞尔曲线生成轨迹：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def genSliderTrace():
        def cubic_bezier_curve(x1, y1, x2, y2, x_cp1=1, y_cp1=2, x_cp2=2, y_cp2=-1, num_points=20):
            # 生成一个从0到1的数列，用于计算贝塞尔曲线上的点
            t = np.linspace(0, 1, num_points)
            points = []

            # 遍历参数t的每个值，计算曲线上对应点的坐标
            for t_val in t:
                # 三次贝塞尔曲线的公式
                x = np.power((1 - t_val), 3) * x1 + 3 * np.power((1 - t_val), 2) * t_val * x_cp1 + \
                    3 * (1 - t_val) * np.power(t_val, 2) * x_cp2 + np.power(t_val, 3) * x2
                y = np.power((1 - t_val), 3) * y1 + 3 * np.power((1 - t_val), 2) * t_val * y_cp1 + \
                    3 * (1 - t_val) * np.power(t_val, 2) * y_cp2 + np.power(t_val, 3) * y2

                # 将计算得到的点添加到列表中
                points.append((x, y))

            # 返回曲线上所有计算得到的点
            return points

        x1, y1 = 0, 0
        # 目标点
        x2, y2 = distance, -1

        t = cubic_bezier_curve(x1, y1, x2, y2, x_cp1=40, y_cp1=20, x_cp2=240, y_cp2=160)
        return t

最后通过验证：