通过数组构造树

通过前序遍历数组(后序遍历数组)和中序遍历数组构造树的方法😀

前序遍历+中序遍历构造

本题为leetcode-105

在前序遍历中，我们可以知道顺序为：中、左、右

在中序遍历中，我们可以知道顺序为：左、中、右

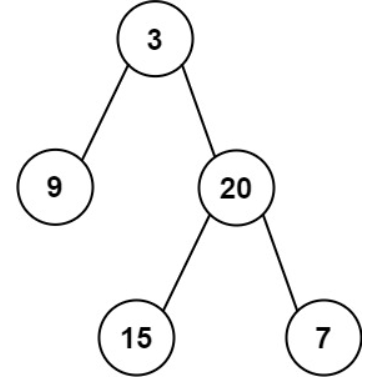
preorder = [3,9,20,15,7];
inorder = [9,3,15,20,7];

如上两个数组，我们可以发现前序数组的第一个元素3就是根节点的数据，那么根据这个根节点的数据，我们可以在中序数组中分割出两个子数组

inorderLeft = [9];
inorderRight = [15,20,7];

接着，我们发现在前序数组中，不能直接分割出后面的左右两部分，需要借助分割出的中序数组来帮助我们分割前序数组，即通过新的两个中序数组的大小，我们可以在前序数组中找出左右子树的区间。

preorderLeft = [9];
preorderRight = [20,15,7];

然后递归左子树和右子树即可。

完整代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        // 先序遍历的为空说明所有节点已经遍历完成
        if (preorder.size() == 0){
            return nullptr;
        }
        // 取先序数组的第一个元素作为根节点
        int value = preorder[0];
        TreeNode * ansTree = new TreeNode(value);
        if (preorder.size() == 1)
        {
            // 叶子节点
            return ansTree;
        }
        int index = 0;
        for (; index < preorder.size() ; ++index){
            if (inorder[index] == value) break;
        }
        // 切割中序数组,左闭右开
        vector<int> inorderLeft = vector(inorder.begin() , inorder.begin() + index);
        vector<int> inorderRight = vector(inorder.begin() + index + 1,inorder.end());
        // 通过切割出来的中序数组大小去切割先序数组,左闭右开
        vector<int> preorderLeft = vector(preorder.begin() + 1, preorder.begin() + inorderLeft.size() + 1);
        vector<int> preorderRight = vector(preorder.begin() + inorderLeft.size() + 1,preorder.end());
        // 通过新的数组构建子树
        ansTree->left = buildTree(preorderLeft,inorderLeft);
        ansTree->right = buildTree(preorderRight,inorderRight);
        return ansTree;
    }
};

后序遍历+中序遍历构造

本题为leetcode-106

在后序遍历中，我们可以知道顺序为：左、右、中

在中序遍历中，我们可以知道顺序为：左、中、右

inorder = [9,3,15,20,7];
postorder = [9,15,7,20,3]

如上两个数组，我们可以发现后序数组的最后一个元素3就是根节点的数据，那么根据这个根节点的数据，我们可以在中序数组中分割出两个子数组

inorderLeft = [9];
inorderRight = [15,20,7];

接着，我们发现在后序数组中，不能直接分割出前面的左右两部分，需要借助分割出的中序数组来帮助我们分割后序数组，即通过新的两个中序数组的大小，我们可以在后序数组中找出左右子树的区间。

postorderLeft = [9];
postorderRight = [15,7,20];

然后递归左子树和右子树即可。

完整代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (postorder.size() == 0)
        {
            return nullptr;
        }
        int value = postorder[postorder.size() - 1];
        TreeNode * ansTree = new TreeNode(value);
        // 找到中序数组分割点
        int index = 0;
        for ( ; index < inorder.size() - 1; ++index)
        {
            if ( inorder[index] == value ) break;
        }
        // 分割中序数组
        vector<int> inorderLeft = vector(inorder.begin(), inorder.begin() + index);
        vector<int> inorderRight = vector(inorder.begin() + index + 1, inorder.end());
        // 分割后序数组
        vector<int> postorderLeft = vector(postorder.begin() ,postorder.begin() + inorderLeft.size());
        vector<int> postorderRight = vector(postorder.begin() + inorderLeft.size() , postorder.end() - 1);
        ansTree->left = buildTree(inorderLeft,postorderLeft);
        ansTree->right = buildTree(inorderRight,postorderRight);
        return ansTree;
    }
};

编码细节

在分割区间时，必须要同一格式，这里我采用的是左闭右开形式。对于vector数组在构造时，是默认左闭右开构造的。

 // 分割中序数组
vector<int> inorderLeft = vector(inorder.begin(), inorder.begin() + index); // 不包含inroder.begin() + index
vector<int> inorderRight = vector(inorder.begin() + index + 1, inorder.end());// 不包含inorder.end()

前序数组和后序数组不能完成构造

没有中序遍历无法确定左右部分，也就是无法分割。

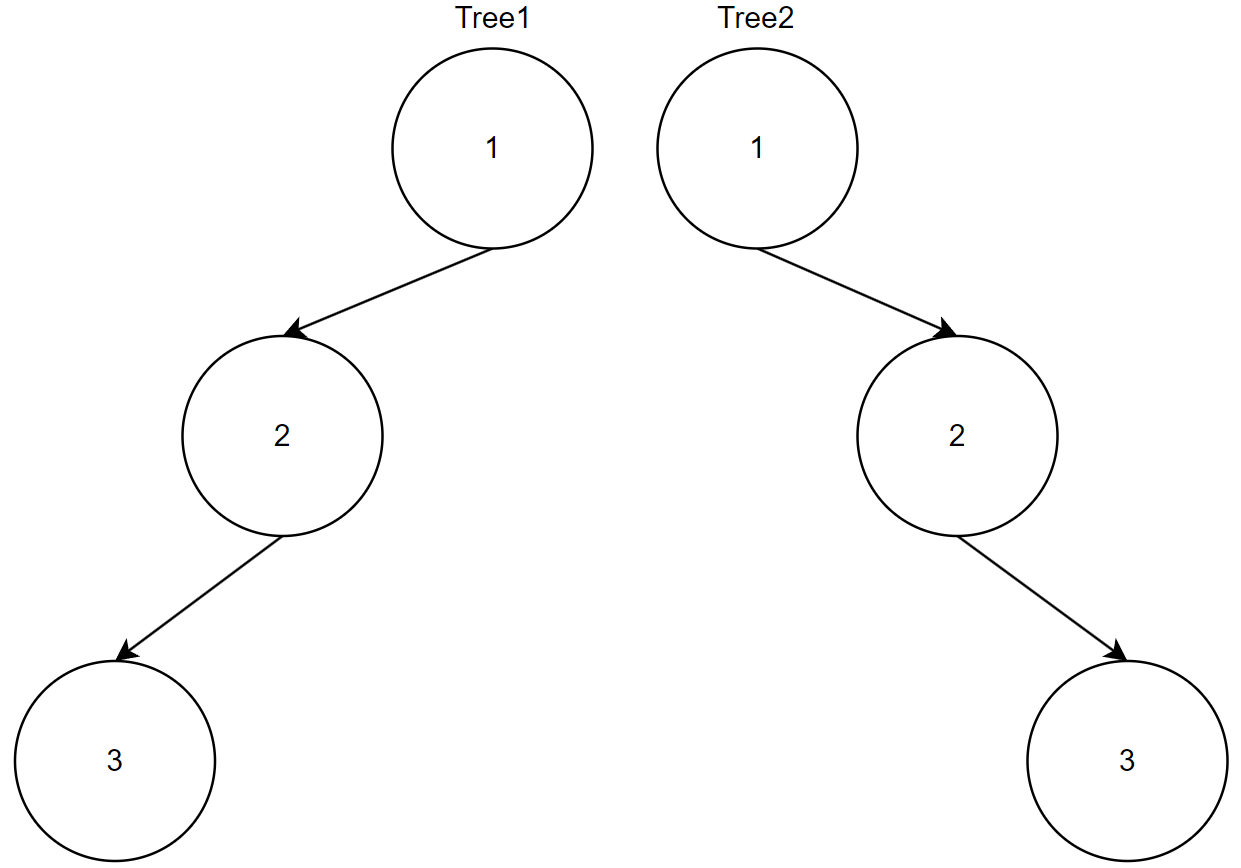
tree1 的前序遍历是[1 2 3]， 后序遍历是[3 2 1]。

tree2 的前序遍历是[1 2 3]， 后序遍历是[3 2 1]。

那么tree1 和 tree2 的前序和后序完全相同，这是一棵树么，很明显是两棵树！