博弈程序编写

写一些博弈相关的东西

基础概念

点格棋由$6655$的格子，整个局面一共25个格子和60条边。

游戏规则：四条边围住一个格子，这个格子归属于放下最后一条边的一方，当最终棋盘被填满时，占据格子多的一方获胜。

长链：一系列尚未被完全围住的正方形（通常只有两条边），这些正方形共享边，形成一个连续的链条状结构。如下图

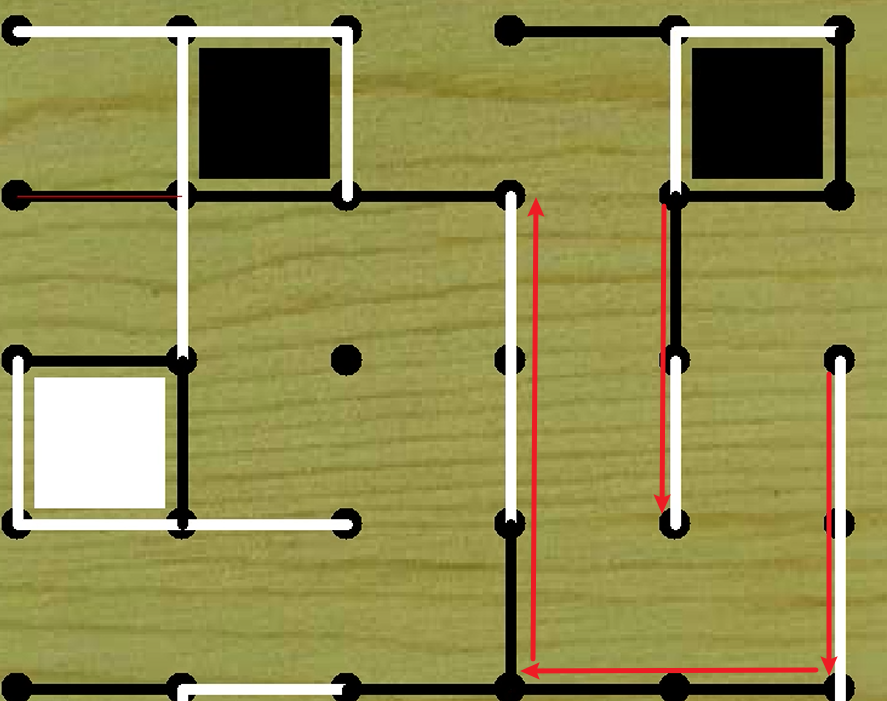
打开长链：当一方使得长链正方形中的某一个正方形构成了3边，就会形成死树，那么其对手方将获会占据所有长链正方形。

死树：一个已经形成的长链状结构，只差一条边就可以完成并将所有包含的正方形“吃完”（即完成所有正方形，获得分数和额外回合）。死树非常接近完成，但当前回合的玩家不愿意去画最后那条边，因为这样做会给对手带来大量得分。

环：若干个正方形围成的闭合结构，即它们的边已经被画满，形成一个封闭的回路。

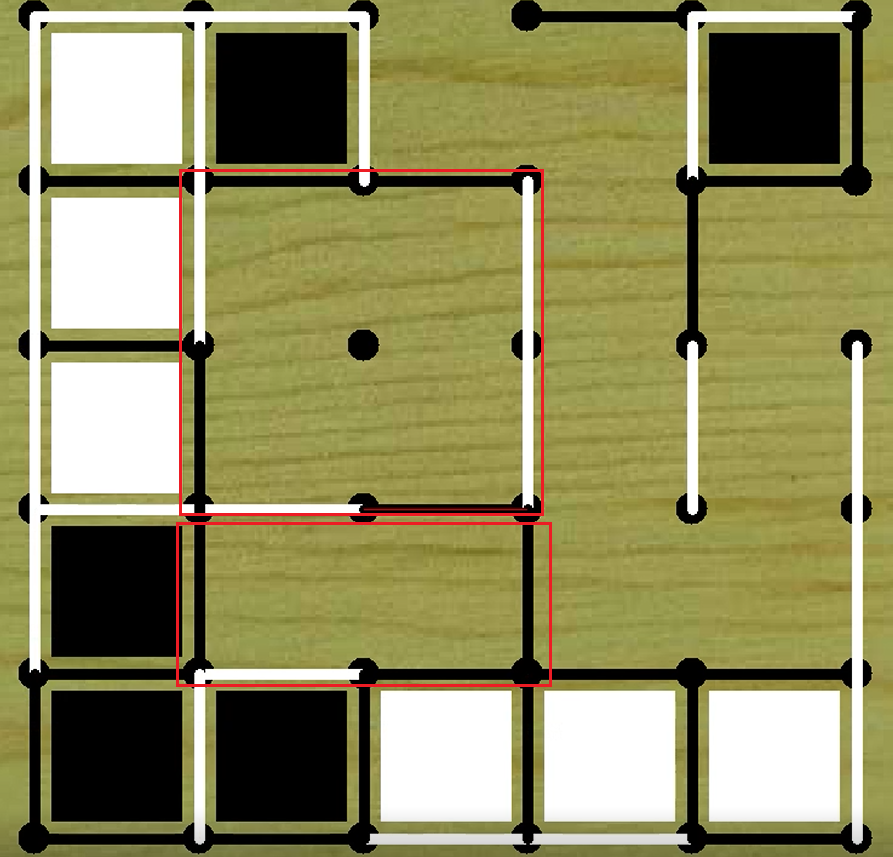
让格：通过不主动完成某些正方形，让对手先操作一些边线，从而为自己留下更有利的操作空间。

alpha&beta剪枝

树结构定义：

每个节点表示此时的赢面

根节点表示我方赢面

父节点到子节点表示执棋方落子一步，故以我方为根节点，则奇数层为我方赢面，偶数层为敌方赢面

搜索深度就是树的深度

最大最小算法：

​ 根据树结构定义，我们显然要在奇数层获取最大赢面，对手会在偶数层使得我们走向最小赢面。故我们在偶数层填入子节点中的最小值，称为MIN节点，在奇数层填写子节点中的最大值，称为MAX节点。

剪枝：

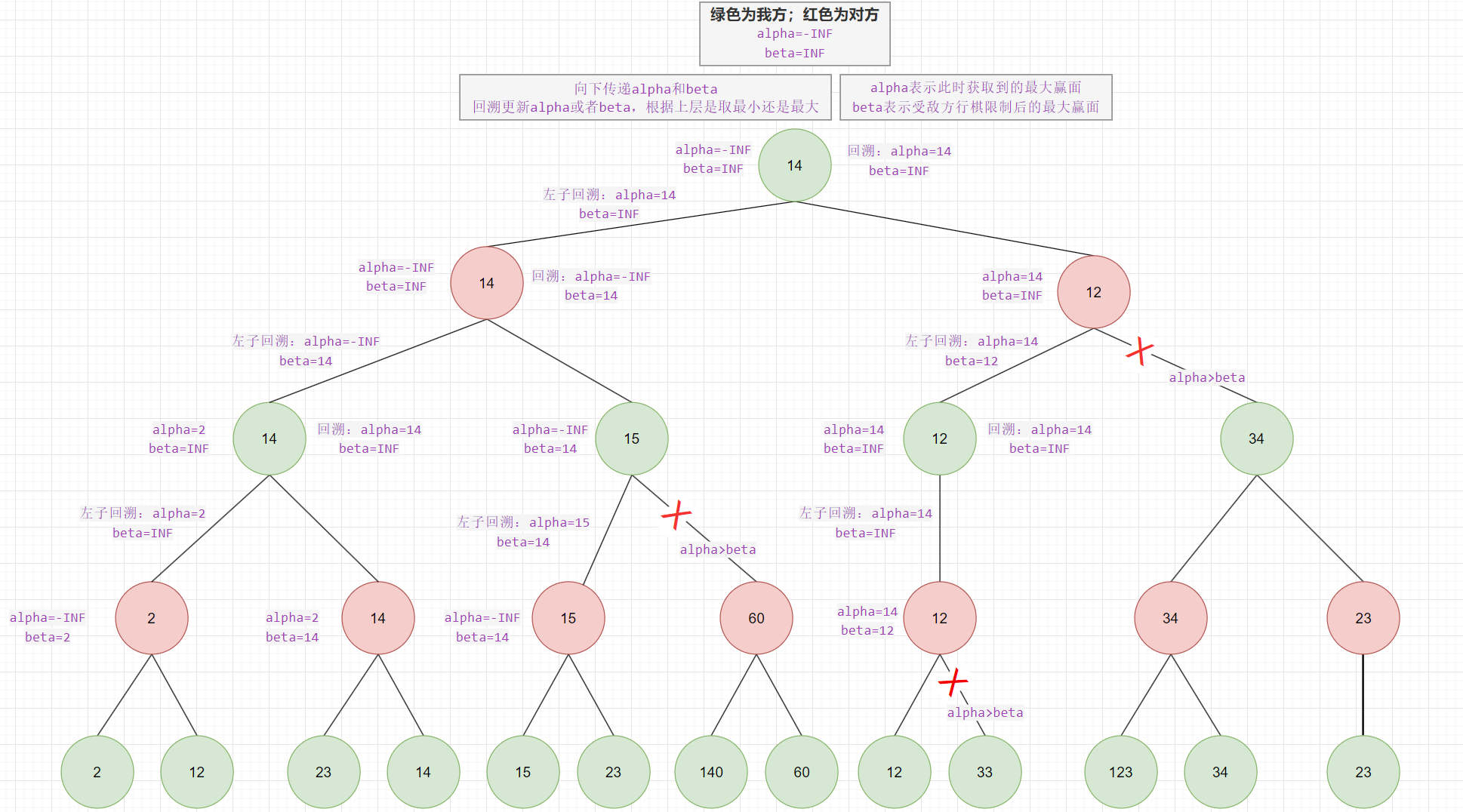
​ 上述算法需要遍历整个博弈树，我们发现在遍历博弈树的过程中，我们的赢面情况是在不断变化的，所以我们可以记录当前赢面的范围，从而规避掉不必要的搜索路径。alpha表示此时可以获得的最大赢面，beta表示此时我方受到敌方行棋限制（根据先前的搜索结果敌方可以导向我方选择路径）后可以获得的最大赢面，当alpha大于等于beta时，剪掉后续路径。

回溯过程中存在三种状态：

1. 初始状态：通过父节点向下传递alpha和beta的值
2. 左子树回溯结果：如果是MAX节点，则更改alpha的值，需要满足值大于原alpha，否则不用更改；如果是MIN节点，则更改beta的值，需要满足值小于原beta，否则不用更改
3. 回溯结果：即右子树回溯，

蒙特卡洛树搜索

当时，

当时，

当时，

当时，

UCB计算公式：
$$
r_i=v_i+c\sqrt{\frac{2ln(\sum_{i}T_i)}{T_i}}
$$

优化估值方法

在游戏的中后期，会出现让格的情况，即牺牲一次围住格子的机会去换取后续更多的格子数。如何判断是否让格是个很大的问题，不妨这样想，

• 环和长链越多，则空格多，说明我方应该优先填充仅剩的边线，让对手填充环和长链形成死树，可以让格。
• 当前空格少时，环和长链越少，此时应该由当前剩余格子数决定。

我这里设置一个控制值，当时，表示可以让格。
$$
c(G)=size(G)-4longChain-8loops+tb(G)
$$

点格棋代码实现

主函数

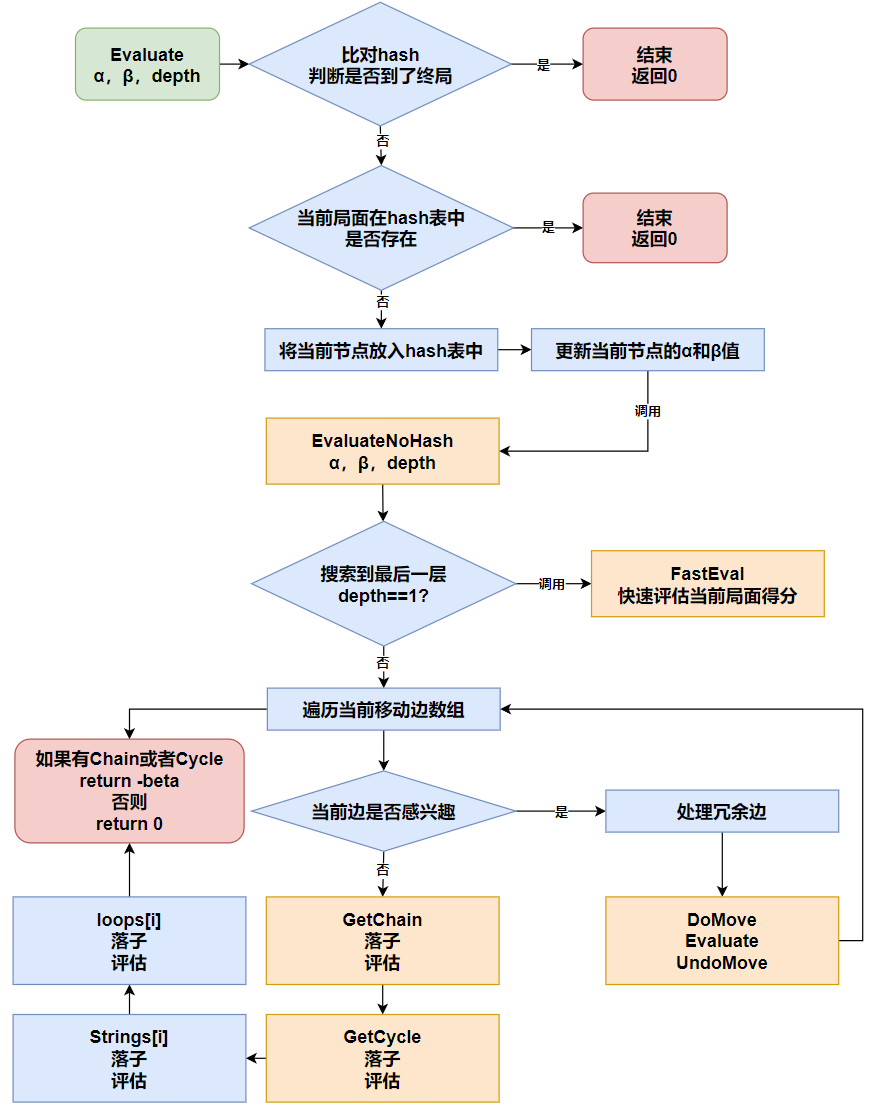
这个函数是博弈引擎与平台进行通信交互的主函数，具体逻辑如下：

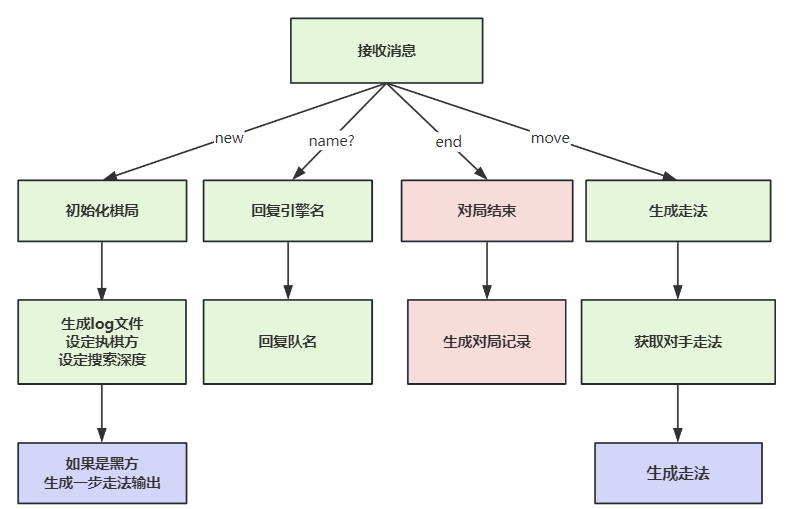
主要行棋逻辑

MyMove()函数主要是清理当前棋局，并产生走法，然后调用评估函数得到评分最大的走法

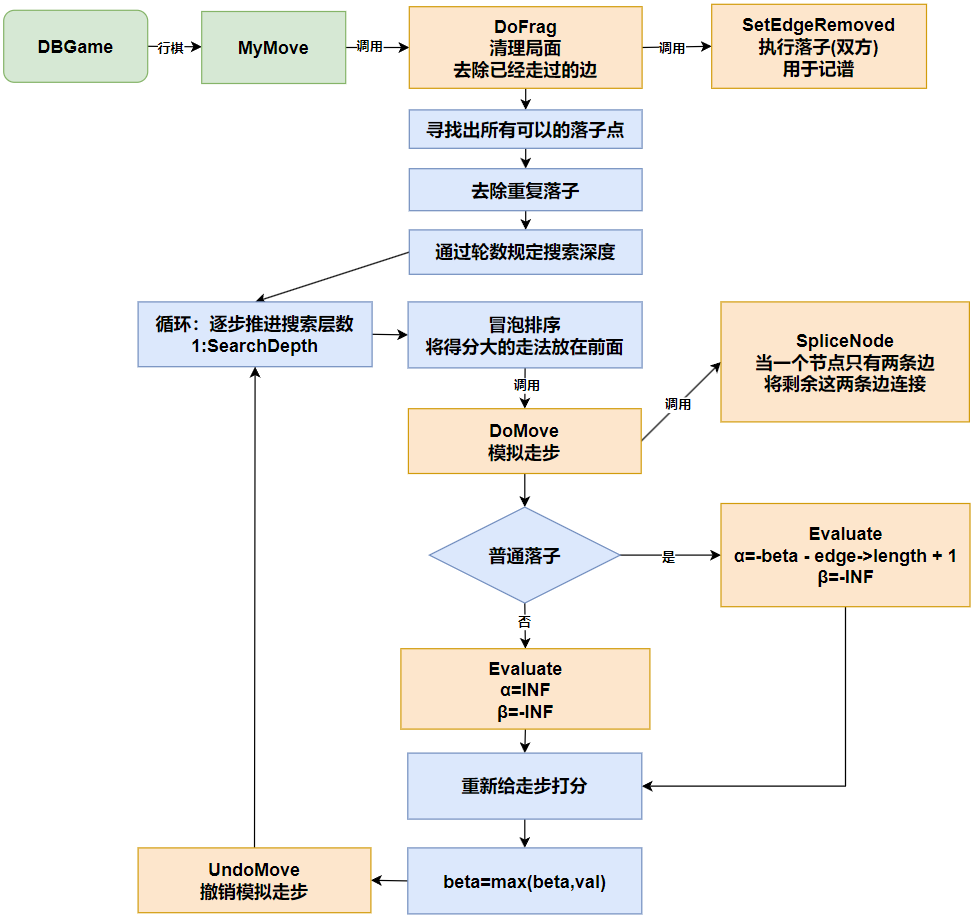
评估函数

主要使用极大极小搜索，以及使用α&β剪枝算法剪枝